JavaScriptCoding challenges

Calculating π within an Infinite-Length List Class

CategoryAlgorithms

Published20 January, 2023

Last updated21 January, 2023

AuthorKelly

I recently encountered a coding challenge requiring the development of a List class capable of handling infinite-length lists. One of the requirements was for the class to include a PI() method to compute the value of π. To address this, I employed generator functions to manage infinity, applying the same concept to the PI() method generator.

Below is an outline of the key methods involved in calculating π:

class List {

   constructor(generator, min = 0, max = Infinity) { /* ... */}

   // Implementation of other list methods...

   get(n) { /* Retrieves a value based on the provided index */ }

   static arctan(x) { /* Generator for the Arctan series */ }

   static get PI() { /* Generator for PI calculation */ }

}

The implementation includes:

The constructor method, which accepts the generator function and stores it for future use.
The arctan method, which takes a parameter x (explained in detail below).
The PI method is a getter, meaning we can directly call it to retrieve values generated by the function.

Let's now examine a few steps leading up to the construction of the arctan(x) method.

Arctan (Trigonometry)

The formula used to create the arctan(x) method derives from the concept of inverse trigonometric functions, with arctan being a key function. While arctan has various applications, I focused specifically on its role in calculating π. Consider the following formula:

const PI = 4 * ( arctan(1/2) + arctan(1/3) );

This is a Machin-like formula to approximate π, specifically derived from Euler's solution, which uses a Taylor series to represent the infinite sum:

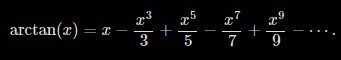
Arctan function with Taylor series

In code, this can be expressed as:

0 + x^1/1 - x^3/3 + x^5/5 - x^7/7 + ... (continues infinitely)

Here is the implementation of the arctan(x) method:

static arctan(x) {
   function* generator() {
      let sum = 0;
      for(let i = 0; true; i++) {
         sum += (Math.pow(-1, i) * Math.pow(x, 2 * i + 1)) / (2 * i);
         yield sum;
      }
   }
   return new List(generator);
}

To clarify, I'll explain the formula in two parts:

Controlling the sign of each term.
Implementing the Taylor series formula.

Controlling the Sign of Each Term

By using a counter variable (i), I was able to alternate between positive and negative signs for each term in the series with the following code:

Math.pow(-1, i)

// Examples
console.log(Math.pow(-1, 0)); //  1
console.log(Math.pow(-1, 1)); // -1
console.log(Math.pow(-1, 2)); //  1
console.log(Math.pow(-1, 3)); // -1

The sum operator += automatically handles the current term's sign based on the iteration.

Implementing the Taylor Series Formula

The code representing each term in the series, such as x^1/1, is as follows:

Math.pow(x, 2 * i + 1) / (2 * i);

Each term is added to the sum variable, storing the cumulative result:

sum += (Math.pow(-1, i) * Math.pow(x, 2 * i + 1)) / (2 * i);

Implementing the `PI()` Method

With the arctan(x) method in place, implementing the PI() method was straightforward. As mentioned earlier, I used Euler's formula to calculate π:

static get PI() {
   function* generator() {
      let counter = 0;
      let pi = 0;
      yield pi;
      // Euler's formula:
      const [ arc1_2, arc1_3 ] = [ List.arctan(1 / 2), List.arctan(1 / 3) ];
      while(true) {
         // PI = 4 * ( arctan(1/2) + arctan(1/3) )
         pi = 4 * (arc1_2.get(counter) + arc1_3.get(counter));
         yield pi;
         counter++;
      }
   }
   return new List(generator);
}

Final Calculation of π

The most challenging aspect was managing the approximation in test cases. However, once the List class was fully implemented, it could be used as follows:

console.log(List.PI.get(1));   // 3.333333333333333
console.log(List.PI.get(5));   // 3.1417411974336886
console.log(List.PI.get(12));  // 3.1415926497167876
console.log(List.PI.get(100)); // 3.1415926535897922